Cálculo do CDI no Sql Server - Scripts
Este post é a 2ª parte de uma série tratando da implementação, diretamente no Sql Server, do cálculo do fator acumulado do CDI (ou Selic). A 1ª parte tratou da teoria por trás dos cálculos e introduziu algumas questões relativas à precisão que podem afetar o peso da computação.
Um repositório contendo o código completo desta implementação está em nosso GitHub, caso deseje ir direto ao resultado. No post explicaremos em detalhes a implementação e suas limitações.
Licença do código
Todo código apresentado aqui é livre para uso, em qualquer tipo de aplicação, por qualquer pessoa ou instituição. Podendo ser incorporado no todo, ou em parte, modificado ou não, em qualquer software, privado ou público, distribuído por qualquer licença. No entanto, não há qualquer garantia, nem mesmo quanto a correção, aplicabilidade e segurança. Em nenhuma circunstância a Elekto será responsável por qualquer tipo de perda, incluindo, mas não limitando-se a, financeira, de reputação ou de vidas devido ao uso correto, ou não, do código fornecido livremente neste artigo.
Formalmente, todo código aqui usa a licença MIT conforme abaixo:
The MIT License (MIT)
Copyright © 2022 Elekto Produtos Financeiros Ltda.
Permission is hereby granted, free of charge, to any person obtaining
a copy of this software and associated documentation files
(the “Software”), to deal in the Software without restriction,
including without limitation the rights to use, copy, modify, merge,
publish, distribute, sublicense, and/or sell copies of the Software,
and to permit persons to whom the Software is furnished to do so,
subject to the following conditions:
The above copyright notice and this permission notice shall be
included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED “AS IS”, WITHOUT WARRANTY OF ANY KIND,
EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES
OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND
NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS
BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER
IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT
OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
DEALINGS IN THE SOFTWARE.
Se não estiver confortável em usar código deste artigo sob essa licença, nos procure para negociarmos uma licença alternativa.
Uma implementação Canônica
Criando o Banco de Dados de Teste
Vamos começar criando um banco de dados que servirá para conter nossos testes. Usei Sql Server 2019 15.0.2080.9, mas não existe nada particularmente moderno nos comandos, procedures e funções que serão criadas.
USE [master]
GO
CREATE DATABASE [CdiForFunOrProfit]
ON PRIMARY
( NAME = N'CdiForFunOrProfit', FILENAME = N'C:\DB\CdiForFunOrProfit.mdf' , SIZE = 5MB , MAXSIZE = 100MB , FILEGROWTH = 10MB)
LOG ON
( NAME = N'CdiForFunOrProfit_log', FILENAME = N'C:\DB\CdiForFunOrProfit.ldf' , SIZE = 512KB , MAXSIZE = 100MB , FILEGROWTH = 10%)
WITH CATALOG_COLLATION = DATABASE_DEFAULT;
GO
-- Só testes, não precisamos de recovery completo...
ALTER DATABASE [CdiForFunOrProfit] SET RECOVERY SIMPLE;
GO
use [CdiForFunOrProfit];
GO
-- Um esquema, para ficar mais organizado
create schema [Over];
GO
Não esqueça de ajustar o caminho para os arquivos de dados e logs, conforme sua instância. Para uma performance melhor, coloque log e dados em discos diferentes. Mas nossos testes serão com uma massa relativamente pequena...
Populando uma tabela com o CDI
Naturalmente precisamos de uma tabela contendo a taxa CDI a cada dia para fazermos os cálculos, e ela pode ser tão simples quanto duas colunas, a data e a taxa. Mas lembrando-se da fórmula, já podemos pré-computar, e armazenar permanentemente, o fator do DI diário,
O fator diário, com o arredondamento, é definido como POWER do Sql Server recebe dois floats, e se não forem, faz a conversão implícita. float é a constante 0.003968253968253968 e já colocaremos diretamente em nossa expressão.
Devemos pensar também no tipo de campos que usaremos. Nessa implementação canônica não queremos nenhum arredondamento implícito ou truncagem fora de nosso controle que leve a perdas de precisão, como conversões de decimais para ponto flutuante binários (float) alterando os números.
A maior inflação brasileira ocorreu em Março de 1990 com 81,3% ao mês. Supondo um juros um tanto maior, de 100% a.m., e o anualizando, podemos ter taxas de 410.000% ao ano! Faz sentido reservar, para um CDI futuro (futuro muito sombrio) 6 dígitos para a parte inteira? Pessoalmente, creio que não. E se acontecer, estaremos mais preocupados em arrumar comida, ou emigrar do que procurando estouros em código. Ainda assim vamos deixar com espaço para 6 dígitos inteiros. Um fator 0.03722550694..., portanto para armazenar nossos decimal(9, 8) com tranquilidade. A fórmula especifica que deve haver arredondamento na 8ª casa decimal. O resultante de POWER conterá 13 ou 14 dígitos significativos então resta saber se na conversão de float para decimal(9, 8) ocorre truncagem ou arredondamento. O script abaixo tira a dúvida, e demonstra que nessa coerção teremos arredondamento, o que é excelente.
declare @f float;
set @f = 0.1234567890123456789;
print format(@f, 'G17'); -- dá 0.12345678901234568
declare @d decimal(9, 8);
set @d = @f;
print @d; -- dá 0.12345679, arredondamento, e não truncagem!
Assim, podemos criar nossa tabela para CDI com o script abaixo.
USE [CdiForFunOrProfit];
GO
CREATE TABLE [Over].[Cdi]
(
[Date] [date] NOT NULL,
[Rate] [decimal](8, 2) NOT NULL,
[DailyFactor] as (cast((power([Rate]/100 + cast(1 as float), 0.003968253968253968) - 1) as decimal(9, 8))) persisted,
CONSTRAINT [PK_Over_Cdi] PRIMARY KEY CLUSTERED
(
[Date] ASC
) WITH (DATA_COMPRESSION = PAGE)
);
GO
-- Só para testar com um número em particular...
insert into [Over].Cdi ([Date], Rate) values ('2021-07-30', 4.15);
select DailyFactor from [Over].Cdi where [Date] = '2021-07-30'; -- 0.00016137 é o esperado.
GO
Nada tão especial, apenas o uso de compressão (menos I/O), e a marcação da coluna DailyFactor como persisted de modo que uma vez calculado os valores, eles fiquem calculados. Lembre-se que essa tabela, em regime, muda apenas uma vez por dia, com a adição de um novo CDI. Pode ser tentador criar um índice incluindo o DailyFactor, mas é preciso experimentar... em nossas máquina, ao contrário da intuição, a performance degradou-se um pouco.
Finalmente, podemos inserir a série histórica de CDI que usaremos como teste. O script completo está no GitHub, mas é algo como...
use [CdiForFunOrProfit];
GO
-- só para garantir que esteja vazia
truncate table [Over].Cdi;
GO
-- De 2002-01-02 até 2022-03-10
insert into [Over].Cdi ([Date], [Rate])
select '2002-01-02', 19.02 union all
select '2002-01-03', 19.02 union all
select '2002-01-04', 19.03 union all
-- ... muitas e muitas linhas omitidas
select '2022-03-08', 10.65 union all
select '2022-03-09', 10.65 union all
select '2022-03-10', 10.65;
GO
-- Só conferências
select count(1) from [Over].Cdi; -- deve dar 5073
select CHECKSUM_AGG(checksum(Rate)+checksum([Date])) from [Over].[Cdi]; -- deve dar -528629890
select CHECKSUM_AGG(checksum(DailyFactor)) from [Over].[Cdi]; -- deve dar 571554945
GO
... que popula o CDI entre 2002-01-02 e 2022-03-10. Ao final apenas algumas checagens, para garantir que todos os dados entraram corretamente.
Criando a Função Canônica
A ideia é criar uma função escalar no Sql Server que possa ser invocada em qualquer ponto, dentro de uma procedure, de outra função, ou diretamente em comandos DML (select, insert, update etc.) que retorne o fator acumulado do CDI entre duas datas, com o alpha (percentagem do indexador) aplicado, calculado conforme as regras canônicas explicadas no 1º artigo.
O produtório dos fatores diários acumulados, com a truncagem na 16ª casa após cada passo é a parte mais complicada pois:
- Não existe uma função de agregação no Sql Server para produtório;
- Multiplicar 2 números com 16 decimais, e truncar (não arredondar) o resultado na 16ª casa requer algum cuidado para não perder dígitos.
Por 1 e 2 usaremos uma função, com um CURSOR. Como é de se esperar, a performance não será estelar, mas por hora queremos correção, e não performance.
Os inputs da função são a data inicial, a data final, e o alpha. O resultado é o fator acumulado, com 8 decimais (veremos posteriormente quantos dígitos na parte inteira). O alpha é aplicado na fórmula com 2 decimais, restando definir quanto na parte inteira: considerando que já houve papéis (promocionais, verdade) a 1.000% do CDI, razoável desejarmos poder calcular esse tipo de coisa, portanto usaremos decimal(6, 2) para o alpha.
A 1ª parte de cada item do produtório será calcular o fator diário, com o alpha aplicado, e truncar na 16ª casa, conforme
-- testando o maior
declare @alpha decimal(6, 2);
set @alpha = 9999.99; -- o maior alpha permitido (nessa implementação)
declare @df decimal(9, 8);
set @df = 0.03722551; -- o fator diário correspondente ao maior CDI permitido (nessa implementação), 999999.99
declare @dfa decimal(18, 15);
set @dfa = (@df * (@alpha / 100))+1;
print @dfa; -- dá 4.722547277449000
-- testando o menor não-zero
set @alpha = 0000.01; -- o menor alpha permitido (nessa implementação)
set @df = 0.00000001; -- o menor fator diário ainda não-zero
set @dfa = (@df * (@alpha / 100))+1;
print @dfa; -- dá 1.000000000001000
Ou seja, para esse 1º resultado precisamos apenas de decimal(13, 12), o que faz sentido, pois
Para a parte seguinte, multiplicando o acumulado pelo fator diário com o alfa, devemos tomar mais cuidado, truncagem será necessária na 16ª casa e havendo espaço, e não sendo explícito, o Sql Server fará arredondamento, o que não desejamos, como o script a seguir demonstra:
declare @dfa decimal(13, 12);
set @dfa = 4.722547277449; -- o maior fator diário, com o maior alfa aplicado
declare @acc decimal(20 ,16);
set @acc = 4.722547277449; -- aplicado sob si mesmo... inflação de 22x em 2 dias!
declare @acc2check decimal(21, 17);
set @acc2check = @dfa * @acc;
print @acc2check; -- dá 22.302 452 787 740 962 18, truncando chegamos em 22.302 452 787 740 962 1
declare @acc2 decimal(20, 16);
set @acc2 = @dfa * @acc;
print @acc2; -- dá 22.302 452 787 740 962 2 Ops! O Sql Arredondou, e não queremos isso
set @acc2 = round(@dfa * @acc, 16, 1);
print @acc2; -- dá 22.302 452 787 740 962 1, que é o queremos!
Queremos o máximo alcance possível, sem perder nenhum decimal. Já sabemos que precisamos de 16 decimais, mas quantos dígitos na parte inteira? Podemos ir até decimal(38, 16), deixando 22 dígitos na parte inteira? Na verdade não...
declare @dfa decimal(13, 12);
set @dfa = 4.722547277449; -- o maior fator diário, com o maior alfa aplicado
declare @acc decimal(38, 16);
set @acc = 4.722547277449; -- aplicado sobre si novamente...
declare @accNext decimal(38, 16);
set @accNext = round(@acc * @dfa, 16, 1);
print @accNext; -- dá 22.302 452 787 740 960 0 e deveria ser 22.302 452 787 740 962 1. O que houve?
o que ocorreu é que o Sql Server tenta preservar a parte mais significativa, mesmo que ao custo da parte menos significativa, e temos um número com 1 digito inteiro multiplicado com um de 22 dígitos inteiros, o resultado requer 23 dígitos inteiros, e com mais 16 decimais dá um total de 39 dígitos. Como decimal só suporta 38, ele irá matar dígitos à direita. Precisamos reduzir o número total de dígitos para deixar espaço de manobra, e suficiente para que não ocorra nenhum arredondamento automático.
declare @dfa decimal(13, 12);
set @dfa = 4.722547277449; -- o maior fator diário, com o maior alfa aplicado
declare @acc decimal(35, 16);
set @acc = 4.722547277449;
declare @accNext decimal(35, 16);
set @accNext = round(@acc * @dfa, 16, 1);
print @accNext; -- dá 22.302 452 787 740 962 1, o que desejamos!
Dá certo! E nos deixa chegar até fatores acumulados com 19 dígitos na parte inteira. Que tal multiplicar seu patrimônio (ou sua dívida) por quintilhões aplicando no CDI?
Assim, temos a assinatura de nossa função, seu tipo de retorno, e o que devemos usar nos acúmulos intermediários para maximizar o alcance sem perder a precisão. Só escrever!
use [CdiForFunOrProfit];
GO
-- Função canônica para o acúmulo de CDI Preciso (Regras B3, CETIP, CRT4 etc)
create or alter function [Over].GetCdiFactorCanon
(
@start date,
@end date,
@alpha decimal(6, 2)
)
returns decimal(27, 8)
with SCHEMABINDING
as
begin
-- resultado final, com 8 casas, arredondado
declare @ret decimal(27, 8);
-- o resultado acumulado é arredondado a partir de um acumulado com 16 casas truncadas
declare @acc decimal(35, 16);
set @acc = 1;
declare @dailyFactor decimal(9, 8); -- já pré-computado na série do CDI
declare @dailyFactorApha decimal(13, 12); -- não precisa de mais alcance e precisão que isso
declare overCursor cursor FAST_FORWARD LOCAL for
select [DailyFactor] from [Over].[Cdi] (nolock)
where
[Date] >= @start -- data inicial inclusive
and [Date] < @end -- data final exclusive
order by [Date] asc; -- não esqueça a ordenação explícita!
open overCursor;
fetch next from overCursor into @dailyFactor;
while @@FETCH_STATUS = 0
begin
set @dailyFactorApha = (@dailyFactor * (@alpha / 100))+1; -- sem necessidade alguma de truncar
set @acc = round(@acc * @dailyFactorApha, 16, 1);
fetch next from overCursor into @dailyFactor;
end;
close overCursor;
deallocate overCursor;
set @ret = ROUND(@acc, 8); -- arredondado
return @ret;
end;
GO
Simples, direta e com um CURSOR... mas estará correta? Podemos conferir com a calculadora fornecida pela B3, mas sim, nossa função funciona:
use [CdiForFunOrProfit];
GO
-- Bate com a B3?
select [Over].GetCdiFactorCanon('2002-01-02', '2022-03-11', 100) union all -- deve dar 8.95486752
select [Over].GetCdiFactorCanon('2002-01-02', '2022-03-11', 300) union all -- deve dar 715.68604111
select [Over].GetCdiFactorCanon('2002-01-02', '2022-03-11', 0.01) union all -- deve dar 1.00021930
select [Over].GetCdiFactorCanon('2021-07-30', '2021-08-02', 250); -- deve dar 1.00040343
-- Yep! Bate.
-- Até quanto do CDI podemos ir por um muito longo período?
select [Over].GetCdiFactorCanon('2002-01-02', '2022-03-11', 400); -- mais do que a calculadora da B3 permite
select [Over].GetCdiFactorCanon('2002-01-02', '2022-03-11', 1000); -- cuidado ao emitir CDBs promocionais...
select [Over].GetCdiFactorCanon('2002-01-02', '2022-03-11', 2005); -- parabéns! você é dono do mundo! Ou o deve...
select [Over].GetCdiFactorCanon('2002-01-02', '2022-03-11', 2006); -- demais! Arithmetic overflow error converting numeric to data type numeric
GO
Eliminando o Cursor, ou não...
É tentador, logo de início, eliminar o CURSOR, que certamente não terá boa performance, calculando e atualizando a variável de acúmulo, @acc, de modo recursivo, algo como:
--... omitido
declare @acc decimal(35, 16);
set @acc = 1;
SELECT
@acc = round(@acc * cast((dailyFactor * (@alpha / 100))+1 as decimal(13,12)), 16, 1)
FROM [Over].[Cdi] (nolock)
where
[Date] >= @start -- data inicial inclusive
and [Date] < @end -- data final exclusive
order by [Date]; -- a ordem é importante!
-- ...omitido
Mas isso não garante que os resultados sejam corretos, é uma má-prática, conforme a Microsoft avisa: "In this case, it is not guaranteed that `@Var` would be updated on a row by row basis. For example, `@Var` may be set to initial value of `@Var` for all rows. This is because the order and frequency in which the assignments are processed is nondeterminant.". E é o que obtivemos em nossos testes: alguns resultados corretos, mas a maioria bastante incoerente. Talvez funcione em outros gerenciadores de Banco de Dados... se descobrir nos avise, por favor.
Testando a Performance
Criando uma massa de testes
Vamos criar uma massa de testes grande o suficiente para brincarmos com nossa função, e vermos o quanto podemos extrair dela.
use [CdiForFunOrProfit];
GO
-- Cria a tabela para conter a massa de testes
create table [Over].Input
(
BatchId char(4) not null, -- para separar execuções diferentes
Id bigint not null identity(1, 1), -- um id único para o registro a ser calculado
[Start] date not null,
[End] date not null,
[Alpha] decimal(6, 2) not null,
CONSTRAINT [PK_Over_Input] PRIMARY KEY CLUSTERED
(
BatchId ASC,
Id ASC
) with (data_compression = page)
);
GO
E vamos a popular com 10 mil fatores a calcular, espalhados uniformemente ao longo de 10 anos entre 2012-03-11 e 2022-03-11, com alphas entre 70% e 300%. Certamente uma amostra bem mais pesada em termos de idade dos papéis do que é normalmente observado. Para um teste realista você deve tentar reproduzir uma distribuição que seja condizente com os portfólios reais a serem tratados. Aqui, queremos um exemplo pesado intencionalmente.
use [CdiForFunOrProfit];
GO
set nocount on;
-- Popula com Registros Aleatórios de prazos variados cobrindo todo o range de modo uniforme
-- Para testes realistas, mimetize a distribuição de idade dos papéis em lote a computar
declare @batchId char(4);
set @batchId = 'In01';
declare @maxDate date;
set @maxDate = '2022-03-11'; -- pode ser um dia útil a mais que o CDI mais atual
declare @minDate date;
set @minDate = '2012-03-11'; -- 10 anos, para CDI, já é um bocado
declare @maxDays int;
set @maxDays = DATEDIFF(day, @minDate, @maxDate);
declare @minAlpha float;
set @minAlpha = 70.0; -- menor alpha
declare @maxAlpha float;
set @maxAlpha = 300.0; -- maior alpha
declare @chanceAlpha100 float;
set @chanceAlpha100 = 0.30; -- chance do Alpha ser exatamente 100%
declare @sampleSize int;
set @sampleSize = 10000; -- vamos começar com calma...
print 'Data Mínima: ' + convert(char(10), @minDate, 23);
print 'Data Máxima: ' + convert(char(10), @minDate, 23);
print 'Prazo Máximo: ' + cast(@maxDays as varchar(5));
print 'Amostras: ' + cast(@sampleSize as varchar(20));
declare @alpha decimal(6, 2);
declare @start date;
declare @age int;
print 'Rand Inicial: ' + cast(rand(22) as varchar(15)); -- para ficar repetitiva a criação
declare @done int;
set @done = 0;
while (@done < @sampleSize)
begin
set @age = rand() * @maxDays;
set @start = DATEADD(day, -@age, @maxDate);
set @alpha = 100.0;
if (rand() > @chanceAlpha100)
begin
set @alpha = @minAlpha + ((@maxAlpha - @minAlpha) * rand());
end;
insert into [Over].Input (BatchId, [Start], [End], [Alpha]) values (@batchId, @start, @maxDate, @alpha);
set @done = @done + 1;
end;
print 'Done!'
GO
select count(1) as Num, AVG(Alpha) as AvgAlpha, AVG(DateDiff(day, [Start], [End])) as AvgAge from [Over].Input where BatchId = 'In01';
-- deve dar 10000 159.730883 1809
GO
E vamos criar uma tabela para conter o resultado dos cálculos...
use [CdiForFunOrProfit];
GO
create table [Over].[Output]
(
BatchId char(4) not null,
Id bigint not null,
[Factor] decimal(38, 8) not null,
CONSTRAINT [PK_Over_Output] PRIMARY KEY CLUSTERED
(
BatchId ASC,
Id ASC
) with (data_compression = page)
);
GO
Medindo a função canônica
Finalmente, vamos popular a tabela de resultados com select e insert, e medir o tempo de execução:
use [CdiForFunOrProfit];
GO
delete [Over].[Output] where BatchId = 'In01';
-- limpar buffers, teste do zero
CHECKPOINT;
DBCC DROPCLEANBUFFERS;
set nocount on;
declare @start datetime;
declare @end datetime;
declare @count bigint;
set @start = GETUTCDATE();
insert into [Over].[Output] (BatchId, Id, Factor)
select
i.BatchId, i.Id, [Over].GetCdiFactorCanon(i.[Start], i.[End], i.Alpha)
from [Over].Input i
where i.BatchId = 'In01';
set @count = @@ROWCOUNT;
set @end = GETUTCDATE();
declare @delta int;
set @delta = DATEDIFF(ms, @start, @end); --ms
declare @speed float;
set @speed = @count * 1000.0E0 / @delta; -- calculos/s
print 'Feitos ' + FORMAT(@count, 'N0') + ' cálculos em ' + FORMAT(@delta, 'N0') + 'ms. Velocidade: ' + format(@speed, 'N1') + ' cálculos/s';
GO 5
Num Sql Server 2019 identificado como Microsoft SQL Server 2019 (RTM-GDR) (KB4583458) - 15.0.2080.9 (X64) ... Developer Edition (64-bit) on Windows 10 Enterprise 10.0 <X64> (Build 22000), rodando num Dell G7, 32GB de RAM, 6 cores, hyperthreading ligado, CPU Intel Core i7 8750H, SSD Micron 1100 SATA de 256GB, nenhuma outra carga na máquina, obtivemos:
| Execução | Tempo (ms) | Velocidade (calculos/s) |
|---|---|---|
| #4 | 83.304 | 120,0 |
| #1 | 81.737 | 122,3 |
| #3 | 81.757 | 122,3 |
| #5 | 81.570 | 122,6 |
| #2 | 81.307 | 123,0 |
| Média (ex Max e Min) | 81.688 | 122,4 |
Não é tão catastrófico... a não ser que seja preciso calcular 10 milhões desses cálculos toda noite, quando então você irá precisar de 23h.
Uma Implementação mais rápida
Não há muito que se possa fazer com a implementação canônica para a melhorar. Pode-se, claro, separar o lote em n partes, correspondentes ao número de CPUs na máquina, e disparar o cálculo em n conexões diferentes, de modo a encher todas as CPUs com a execução. Mas sem muito cuidado na partição dos lotes, e no storage usado podem-se criar contenções de escrita que serão ainda mais custosas.
Um grande problema da implementação canônica é o uso de CURSOR. Sql Server é feito, e otimizado, para processar lógica de conjuntos. Se abrirmos mão das truncagens dentro do produtório interno, e computarmos em float, que tem suporte no hardware para multiplicações, poderíamos usar alguma função de agregação para obter o produtório diretamente.
Não há, porém, uma função de agregação para produtório, MULT, que funcione de modo similar a SUM. Mas isso é contornável com matemática: é possível transformar qualquer produtório numa soma de logaritmos seguida de uma potência, desde que cada termo do produtório seja maior que zero, o que a fórmula e a economia garantem (o alpha não pode ser negativo):
Com isso podemos poderemos trocar o loop por um SUM, como abaixo:
use [CdiForFunOrProfit];
GO
-- Função não-canônica para o acúmulo de CDI, sem a truncagem a cada passo no produtório
-- Mas usando os fatores CDI diários pré-calculados
create or alter function [Over].GetCdiFactorExpSumLn
(
@start date,
@end date,
@alpha decimal(6, 2)
)
returns decimal(27, 8)
with SCHEMABINDING
as
begin
declare @ret decimal(27, 8);
declare @sum float;
select @sum =
SUM
(
LOG
(
1 + DailyFactor * @alpha/100
)
)
from [Over].[Cdi] (nolock)
where
[Date] >= @start -- data inicial inclusive
and [Date] < @end; -- data final exclusive
-- se nenhum dia de CDI se acumulou ainda
if @sum is null
begin
set @ret = 1;
return @ret;
end;
declare @product float;
set @product = EXP(@sum);
set @ret = ROUND(@product, 8); -- arredondado
return @ret;
end;
GO
E vamos experimentar a performance, usando o mesmo lote de input, mas salvando com uma identificação diferente na saída.
use [CdiForFunOrProfit];
GO
delete [Over].[Output] where BatchId = 'Ix01';
-- limpar buffers, teste do zero
CHECKPOINT;
DBCC DROPCLEANBUFFERS;
set nocount on;
declare @start datetime;
declare @end datetime;
declare @count bigint;
set @start = GETUTCDATE();
insert into [Over].[Output] (BatchId, Id, Factor)
select
'Ix01', i.Id, [Over].GetCdiFactorExpSumLn(i.[Start], i.[End], i.Alpha)
from [Over].Input i
where i.BatchId = 'In01';
set @count = @@ROWCOUNT;
set @end = GETUTCDATE();
declare @delta int;
set @delta = DATEDIFF(ms, @start, @end); --ms
declare @speed float;
set @speed = @count * 1000.0E0 / @delta; -- calculos/s
print 'Feitos ' + FORMAT(@count, 'N0') + ' cálculos em ' + FORMAT(@delta, 'N0') + 'ms. Velocidade: ' + format(@speed, 'N1') + ' cálculos/s';
GO 5
E o resultado é uma diferença brutal:
| Execução | Tempo (ms) | Velocidade (calculos/s) |
|---|---|---|
| #3 | 1.317 | 7.593,0 |
| #5 | 1.226 | 8.156,6 |
| #2 | 1.163 | 8.382,2 |
| #4 | 1.163 | 8.698,5 |
| #1 | 1.140 | 8.771,9 |
| Média (ex Max e Min) | 1.194 | 8.375,2 |
O novo cálculo é 68 vezes mais rápido que o canônico. Os 10 milhões de registros que levariam 23h agora seriam resolvidos em 20 minutos.
Mas estão corretos? Vamos usar os cálculos feitos com o método canônico e o rápido para entender as diferenças.
select
ic.[BatchId], ic.Id, ic.[Start], ic.[End], ic.[Alpha], oc.Factor as FactorCanon, oq.Factor as FactorQuick
from [Over].[Input] ic
inner join [Over].[Output] oc
on ic.Id = oc.Id
inner join [Over].[Input] iq
on iq.BatchId = ic.BatchId and iq.Id = ic.Id
inner join [Over].[Output] oq
on iq.Id = oq.Id
where
ic.BatchId = 'In01' and oc.BatchId = 'In01'
and iq.BatchId = 'In01' and oq.[BatchId] = 'Ix01'
and oc.Factor <> oq.Factor;
E não encontraremos em nossa amostra nenhum caso onde os cálculos deem resultados diferentes. Excelente, não? Vamos procurar onde as duas funções dão resultados diferentes com um script um pouco mais sofisticado. Ele irá fazer um loop para prazos em relação a data máxima e outro para alphas até encontrar as diferenças.
Importante notar que a performance, e a correção dessa função é extremamente sensível. Coisas que, em outras linguagens de programação seriam otimizações, como o calculo uma única vez de
Descobrindo o Limite da Segurança
Primeiro vamos criar uma tabela para conter os resultados da investigação:
use [CdiForFunOrProfit];
GO
-- Cria a tabela que conterá os limites de execução para o algoritmo rápido
create table [Over].[CdiSafeLimits]
(
[Start] date not null,
[End] date not null,
[Alpha] decimal(6, 2) not null,
IsSafe bit not null,
CONSTRAINT [PK_Over_CdiSafeLimits] PRIMARY KEY CLUSTERED
(
[Start] ASC,
[End] ASC,
[Alpha] ASC
) with (data_compression = page)
);
GO
E vamos executar o script que popula essa tabela, investigando com prazos que aumentam 1 ano de cada vez, e alphas iniciando em 50% e seguindo até 1.000%.
use [CdiForFunOrProfit];
GO
set nocount on;
-- Script para procurar os limites de segurança do algoritmo rápido e os salvar em tabela
declare @maxDate date;
set @maxDate = '2022-03-11'; -- pode ser um dia útil a mais que o CDI mais atual
declare @minDate date;
set @minDate = (select min([Date]) from [Over].Cdi);
declare @minAlpha decimal(6,2);
set @minAlpha = 50;
declare @maxAlpha decimal(6, 2)
set @maxAlpha = 1000;
declare @deltaAlpha decimal(6, 2)
set @deltaAlpha = 50;
declare @alpha decimal(6, 2);
declare @factorCanon decimal(27, 8);
declare @factorQuick decimal(27, 8);
declare @isSafe bit;
-- Loop voltando para o passado de ano em ano em relação ao máximo
declare @years int;
set @years = 1;
declare @start date;
set @start = DATEADD(year, -@years, @maxDate);
while (@start >= @minDate)
begin
print 'Procurando limites entre ' + convert(char(10), @start, 23) + ' e ' + convert(char(10), @maxDate, 23) + '(' + cast(@years as varchar(2)) + ' anos) ...';
-- Loop dos Alphas
set @alpha = @minAlpha;
while (@alpha <= @maxAlpha)
begin
set @isSafe = 0;
BEGIN TRY
set @factorCanon = [Over].GetCdiFactorCanon(@start, @maxDate, @alpha);
set @factorQuick = [Over].GetCdiFactorExpSumLn(@start, @maxDate, @alpha);
if (@factorCanon = @factorQuick)
begin
set @isSafe = 1;
end;
END TRY
BEGIN CATCH
-- para pegar overflows
print ERROR_MESSAGE();
set @isSafe = 0;
END CATCH;
print ' Alpha ' + format(@alpha, 'G17') + ': ' + format(@factorCanon, 'G17') + ' == ' + format(@factorQuick, 'G17') + ' ? ' + cast(@isSafe as char(1));
-- Atualiza a tabela de limites (idempotente)
update [Over].[CdiSafeLimits]
set IsSafe = @isSafe
where
[Start] = @start and
[End] = @maxDate and
[Alpha] = @alpha;
if (@@ROWCOUNT <= 0)
begin
insert into [Over].[CdiSafeLimits] ([Start], [End], Alpha, IsSafe) values (@start, @maxDate, @alpha, @isSafe);
end;
set @alpha = @alpha + @deltaAlpha;
end;
set @years = @years + 1;
set @start = DATEADD(year, -@years, @maxDate);
end;
GO
E investigar os resultados com um select...
-- onde não é seguro?
select *
from [Over].CdiSafeLimits
where IsSafe = 0
order by [Start] desc, [End], Alpha;
GO
...para descobrir que com o CDI histórico dos últimos 20 anos (em relação a meados de 2022) o método rápido só encontrará o primeiro problema para o prazo de 12 anos (início em 2010) a mais de 900% do CDI. Para prazos de 20 anos (iniciando em 2002) os problemas começam acima de 400% do CDI. Na prática, exceto para papéis excepcionais, é muito seguro usar o método rápido. Mas vamos examinar melhor, convertendo o resultado numa matriz (com a ajuda de tabelas pivot do Excel):
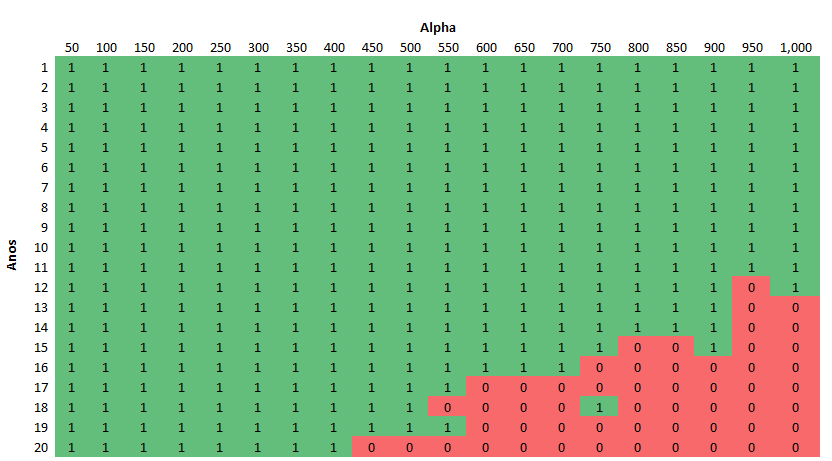
Nota-se que existe uma ampla área segura, mas a fronteira para os não-seguros é fuzzy, borrada. Algumas vezes parâmetros não-seguros ainda dão valores corretos, o arredondamento final simplesmente leva para o mesmo número. Observe que a disposição é em diagonal, como esperado alphas maiores e prazos maiores levam a resultados incorretos na implementação rápida. Vamos plotar, então, Anos x Alpha contra seguro/não seguro:
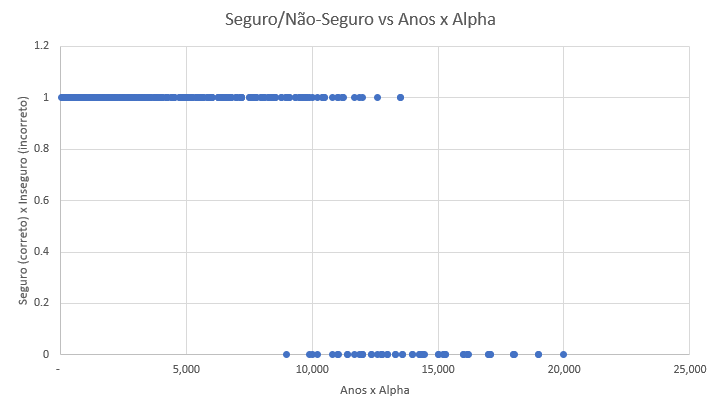
Ou seja, visto a partir de 2022-03-11, se o produto de prazo (em anos) e alpha for menor que 8.800 é seguro usar o algoritmo rápido. E fica muito claro que para a vastíssima maioria dos papéis existentes em 2022, prazos menores que 5 anos, porcentagens do CDI menores que 200%, o algoritmo rápido será preciso.
Para verificar a estabilidade dessa heurística podemos executar o script novamente, mas setando a data final como 2012-03-11, e observar que ainda ficou seguro para Anos x alpha de até 7.000, deixando a heurística simples de 5 anos e 200% ainda bem dentro de limites seguros.
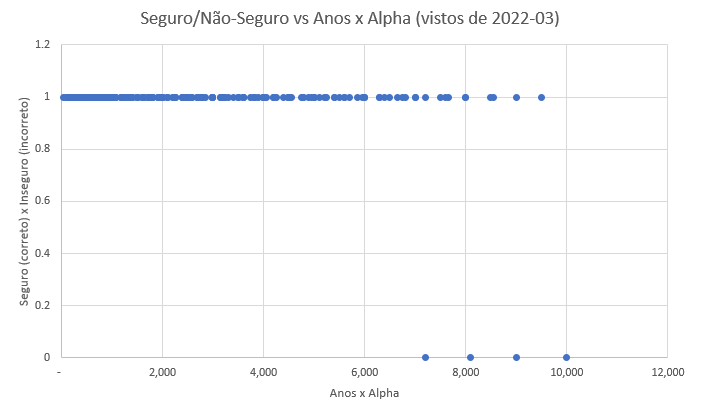
Mas e se os níveis do CDI aumentarem muito no futuro? Na década de 90 (pós Plano Real) o CDI médio foi de ~32%, bem acima do observado em nossa amostra, entre 2002-01-02 e 2022-03-10, de ~12%. Fizemos o experimento, somando em cada valor do CDI de nossa série +25%, de modo que a média do período passou a ser ~37% e rodamos novamente, sob esse cenário mais rigoroso. Ainda assim, nesse cenário distópico, o algoritmo rápido continua seguro até Anos x alpha de 3.200, com boa margem em relação a heurística simples de 5 anos e 200% de alpha.
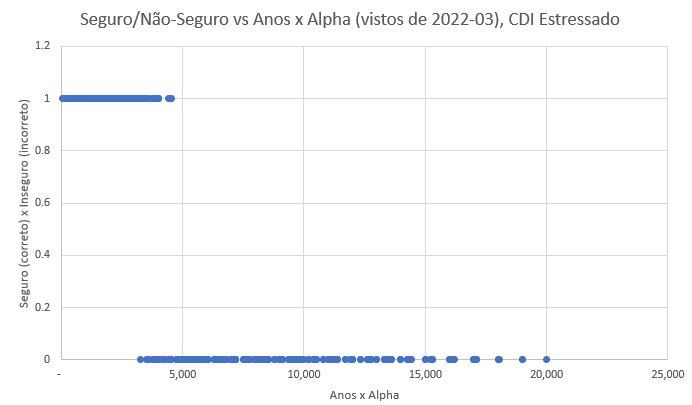
Caso se deseje ainda mais confiança no cálculo, pode-se converter o script que busca os problemas numa procedure, a ser executada toda noite, após a alimentação do novo CDI. E então os resultados dela podem ser usados numa outra função, que consulta antes os limites seguros, e se o forem, invoca a função rápida, e caso contrário invoca a função canônica. Desse modo, ao custo de um lookup rápido, se tem o melhor de todos os mundos: um cálculo rápido, aplicado em quase toda situação normal, e um cálculo rigoroso, a ser aplicado em situações muito especiais.
Conclusões
Nesse artigo apresentamos uma implementação canônica do cálculo do fator de acúmulo do CDI, e demonstramos como, com um truque matemático, pudemos aumentar a velocidade da implementação em mais de 68 vezes. A implementação rápida é também muito confiável, dando os mesmos resultados da implementação canônica, para qualquer papel CDI normal. É apenas com papéis excepcionais (anos rendendo muito mais que 200% do CDI) que os problemas se acumulam, e demonstramos que existem métodos para determinar esses limites seguros e invocar uma ou outra implementação.
No próximo artigo, ainda não publicado, iremos comparar essa implementação com o cálculo externo ao Sql Server, em aplicações .Net e dentro de módulos CLR carregados diretamente no Sql Server, além de explorar possibilidades de paralelismo massivo com o uso de GPUs.

Anteriormente, após cada artigo de nosso blog, havia uma seção de comentários e opções de compartilhamento simples.
Contudo, com a entrada em vigor da LGPD, a coleta de informações pessoais exige consentimento prévio, o que dificulta manter uma interação fluida. Além disso, provedores de comentários e ferramentas de moderação exigem coleta de dados, tornando-nos corresponsáveis ao incorporá-los em nosso site.
Paralelamente, decisões recentes (final de 2024) do STF aumentaram a responsabilidade dos proprietários de sites sobre o conteúdo postado por terceiros, exigindo remoção imediata de conteúdos potencialmente ofensivos, mesmo sem determinação judicial prévia.
Diante desse cenário ruim em termos de Liberdade de Expressão, optamos por encerrar a seção de comentários, visando cumprir a legislação e reduzir riscos operacionais.